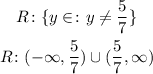5.

1st step
Replace f(x) with y:
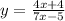
2nd step:
Replace every x with a y and replace every y with an x:
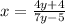
3rd step:
Solve for y:
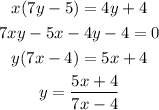
4th step:
Replace y with f^-1(x)

---------------------------------
The domain of f^-1(x) will be given by:

Since we can't divide by zero, so:
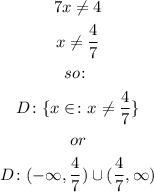
The range of f^-1(x) will be the domain of f(x), the domain of f(x) is given by:

Because we can't divide by zero, so:
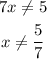
Therefore, the range of f^-1(x) is: