Question

Which of the following is a root of the polynomial function below? F(x) = x2 +6x2 + 12x +7

Answer 1

To find the roots of the given polynomial, here are the steps:

1. Equate the function to zero.

`x^3+6x^2+12x+7=0`

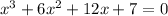
2. Find a value of x that would make the equation zero. By trial and error, we can use x = -1. Let's check if this makes the equation zero. Let's replace x with -1 in the equation above.

`\begin{gathered} (-1)^3+6(-1)^2+12(-1)+7=0 \\ -1+6-12+7=0 \\ 0=0 \end{gathered}`

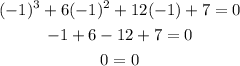
Since the equation is equal to zero when x = -1, we can say that (x + 1) is a factor of the polynomial.

3. Let's find the other factor. To get the other factor of the polynomial, let's divide the polynomial by (x + 1) using synthetic division.

Hence, the other factor of the polynomial is (x² + 5x + 7).

4. Equate the other factor to zero and find the value of x. Use quadratic formula.

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In the second factor, a = 1, b = 5, and c = 7. Let's plug this in to the formula above.

`x=\frac{-5\pm\sqrt[]{5^2-4(1)(7)}}{2(1)}`

Simplify.

`\begin{gathered} x=\frac{-5\pm\sqrt[]{25-28}}{2} \\ x=\frac{-5\pm\sqrt[]{-3}}{2} \\ x=\frac{-5\pm i\sqrt[]{3}}{2} \end{gathered}`

Therefore, the roots of the given polynomial are x = -1 and x = (-5 ± i√3)/2 as shown above.

Based on the options, only Option B is a root of the given polynomial.