Question

Use the given zereo to find the remaining zereos of the function.

Answer 1

Given the function:

`f(x)=x^3-5x^2+36x-180`

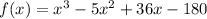
The given function has 3 zeros

one of the zeros = -6i

so, the second one will be a conjugate to the first zero

So, the second one = 6i

The product of the three zeros = -180

let the third zero = a

So,

`\begin{gathered} -6i\cdot6i\cdot b=-180 \\ -36i^2\cdot b=180 \\ -36\cdot-1\cdot b=180 \\ 36b=180 \\ \\ b=(180)/(35)=5 \end{gathered}`

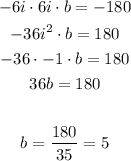
So, the third zero = 5

So, the answer will be:

The remaining zeros of the function are: 6i and 5