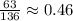Question

A manutacturing company performs a qualty control analysis on the ceramic tile it produces Suppose a batch of 17 tiles has 7 defective tiles. It 3 tiles are sampled at random what isthe probability that exactly 1 of the sampled tiles is defective?How many ways can 3 tles be selected from 17 ties?(Type a whole number)Help Me Solve ThisView an ExampleGet More HelpClear AllCheck Answer

Answer 1

Let A be the event that exactly one of the sampled tiles is defective.

In a batch of 17 tiles, 7 are defectives.

3 tiles are sampled at random.

3 tiles can b eselected from 17 tiles in

`^(17)C_3=680`

ways.

Therefore, the number of points in sample space is 680.

Now, 1 defective item can be selected from 7 defetctive items in 7 different ways. For each of these ways, remaining two items can be selected from (17-7)=10 non-defective items in

`^(10)C_2=45`

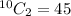
ways.

Therefore, from the batch of 17 tiles, 3 items can be selected so that exactly one item is defective in

`45*7=315`

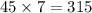
ways.

Therefore, total number of points in sample space in favour of the event A is 315.

By classical definition of probability,

`\begin{gathered} P(A)=(315)/(680) \\ =(63)/(136) \end{gathered}`

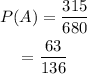
Hence, the probability that exactly 1 of the sampled tiles is defective is

`(63)/(136)\approx0.46`