Question

There are n personal checks made out in the name of n individuals whose names appear n envelopes. Find a recurrence relation for the number of ways these checks can be place in the n envelopes so that no check is in the right envelope.

Answer 1

Let's assume there are 3 personal checks and individuals

First let's find the recurrence relation for the number of ways these checks can be place in the right envelope

`P=(1)/(3)*(1)/(2)*(1)/(1)`

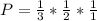
Explanation: Person A has a 1/3 chance of getting the right envelope, person B has a better chance of 1/2 since envelope A is already taken, and finally, person C has a 1/1 chance

Thus, we can also write this as,

`P=(1)/(3!)`

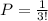
Now, to find the recurrence relation for the number of ways these checks can be place in the n envelopes so that no check is in the right envelope, we just need to substrac 1 - P , which is,

`1-(1)/(3!)`

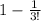
now, we can replace n = 3 and have a general formula,

`1-(1)/(n!)`

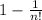
And that's our answer!

1 - 1/n!