A function is defined to be even if it meets the following condition;
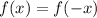
Meaning it is symmetrical about the y-axis.
A functiion is defined to be odd if it meets the condition;
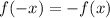
And neither even or odd if it doesnt meet any of the above criteria.
Let us look at sinx.
A well known theorem from sin trigonometry is;

Therefore, sinx is an odd function.
Let us look at cotx.
cot x is defined as;

cosx is an even function, sinx however is odd, so cotx is odd.
Therefore, cotx is an odd function.