The given function is:
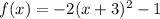
This is a quadratic function or parabola writen in "vertex form"
From the general structure of the vertex form we know that:
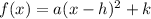
"h" is the x-coordinate of the vertex, in the formula it appears with the sign inverted, this means that if the value is positive, the coordinate will ve negative, or, if the value is negative, then the coordinate will be positive.
"k" is the y-coordinate of the vertex
The sign of "a" indicates if the parabola opens upwards or downwards.
If a is negative → the parabola opens downwards
If a is positive → the parabola opens upwards
So, for the given function:
From this we can determine that the vertex of the quadratic function is:
V(-3,-1)
And its range is
[-∞≤y≤-1] or y≤-1
The domain of these type of functions is all real numbers