Question

An oil tank is being filled at a constant rate. The depth of the oil is a function of the number of minutes the tank has been filling, as shown in the table. Find the depth of the oil 45 minutes after filling begins. Time(min) Depth(ft) 0: 3 10:5 15:6 45 minutes after filling begins, the depth of the oil is feet.

Answer 1

An oil tank is being filled at a constant rate.

In 0 minute, the depth of oil in the tank is 3, : (0,3)

In 10 minute, the depth of oil in the tank is 5, : ( 10, 5 )

In 15 minutes, the depth of oil in the tank is 6, : ( 15, 6 )

Since, the oil is filled at the constant rate, so the equation form by the depth of oil with the time is linear equation.

The general expression for the linear equation is :

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

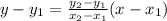
Let x express the time and y express the depth of oil

Substitute any two set of value of time and depth from the table : ( 0, 3) & ( 10, 5 )

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-3=(5-3)/(10-0)(x-0) \\ y-3=(2)/(10)x \\ y-3=(1)/(5)x \\ 5(y-3)=x \\ 5y-15=x \\ x-5y+15=0 \end{gathered}`

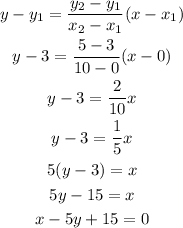
Since, we need to depth of the oil after, 45 minutes,

Substitute x = 45 in the equation :

`\begin{gathered} x-5y+15=0 \\ 45-5y+15=0 \\ 60-5y=0 \\ 5y=60 \\ y=(60)/(5) \\ y=12 \end{gathered}`

as, y represent the depth of the oil

so, depth of the oil is 12 ft in 45 minutes

45 minutes after filling, the depth of the oil is 12 ft

Answer : 45 minutes after filling, the depth of the oil is 12 ft