From the word problem, we can do the following sketch:
Central angle
A wheel has a total angle of 360°. Since the wheel has 20 cars attached to its center, the central angle between any two cars is 18°.
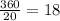
Arc length
The formula to find the arc length in degrees is:

So, in this case, we have:
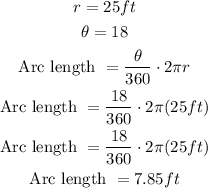
Therefore, the arc length between any two cars rounded to the nearest hundredth is 7.85 feet.
Area of sector
The formula to find the area of a sector in degrees is:
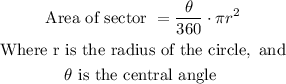
So, in this case, we have:

Therefore, the area of a sector between any two cars rounded to the nearest hundredth is 98.17 square feet.