Question

3.(09.04 MC)A camival ride is in the shape of a wheel with a radius of 25 feet. The wheel has 20 cars attached to the center of the wheel. What is the central angle,arc length, and area of a sector between any two cars? Round answers to the nearest hundredth if applicable. You must show all work and calculationsto receive credit. (10 points)в іU Font Family- AAA ===+V1sagil

Answer 1

From the word problem, we can do the following sketch:

Central angle

A wheel has a total angle of 360°. Since the wheel has 20 cars attached to its center, the central angle between any two cars is 18°.

`\frac{360\text{\degree}}{20}=18\text{\degree}`

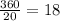
Arc length

The formula to find the arc length in degrees is:

`\begin{gathered} \text{Arc length }=\frac{\theta}{360\text{\degree}}\cdot2\pi r \\ \text{ Where r is the radius of the circle},\text{ and} \\ \theta\text{ is the central angle} \end{gathered}`

So, in this case, we have:

`\begin{gathered} r=25ft \\ \theta=18\text{\degree} \\ \text{Arc length }=\frac{\theta}{360\text{\degree}}\cdot2\pi r \\ \text{Arc length }=\frac{18\text{\degree}}{360\text{\degree}}\cdot2\pi(25ft) \\ \text{Arc length }=(18)/(360)\cdot2\pi(25ft) \\ \text{Arc length }=7.85ft \end{gathered}`

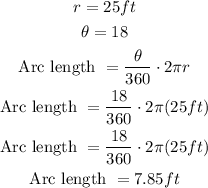
Therefore, the arc length between any two cars rounded to the nearest hundredth is 7.85 feet.

Area of sector

The formula to find the area of a sector in degrees is:

`\begin{gathered} \text{ Area of sector }=\frac{\theta}{360\text{\degree}}\cdot\pi r^2 \\ \text{ Where r is the radius of the circle},\text{ and} \\ \theta\text{ is the central angle} \end{gathered}`

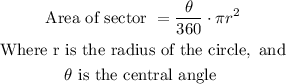
So, in this case, we have:

`\begin{gathered} r=25ft \\ \theta=18\text{\degree} \\ \text{ Area of sector }=\frac{\theta}{360\text{\degree}}\cdot\pi r^2 \\ \text{ Area of sector }=\frac{18\text{\degree}}{360\text{\degree}}\cdot\pi(25ft)^2 \\ \text{ Area of sector }=(18)/(360)\cdot\pi\cdot25^2ft^2 \\ \text{ Area of sector }=(18)/(360)\cdot\pi\cdot625ft^2 \\ \text{ Area of sector }=98.17ft^2 \end{gathered}`

Therefore, the area of a sector between any two cars rounded to the nearest hundredth is 98.17 square feet.