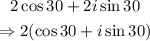Question

ConvertV3 + i to polar form.

Answer 1

`2(\cos 30+i\sin 30)`

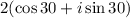
Step-by-step explanation

We want to convert the complex number to polar form:

`\sqrt[]{3}+i`

The general polar form of a complex number is:

`r(\cos \theta+i\sin \theta)`

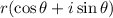
where:

`\begin{gathered} r=\sqrt[]{x^2+y^2} \\ \theta=\tan ^(-1)((y)/(x)) \end{gathered}`

Note: x is the real part of the complex number while y is the coefficient of i.

Therefore, from the number given:

`\begin{gathered} x=\sqrt[]{3} \\ y=1 \end{gathered}`

We now have to find r and θ:

`\begin{gathered} \Rightarrow r=\sqrt[]{(\sqrt[]{3})^2+1^2}=\sqrt[]{3+1} \\ r=\sqrt[]{4} \\ r=2 \\ \Rightarrow\theta=\tan ^(-1)(\frac{1}{\sqrt[]{3}}) \\ \theta=30\degree \end{gathered}`

Therefore, the polar form of the complex number is:

`\begin{gathered} 2\cos 30+2i\sin 30 \\ \Rightarrow2(\cos 30+i\sin 30) \end{gathered}`