Using Coulomb's law
Let:
F1x = Force of the charge of -9.14mC on the charge of -3.78mC
F2x = Force of the charge of -46.31mC on the charge of -3.78mC
So:
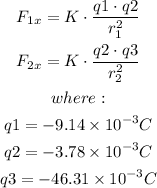
Since the net force on the 3rd charge must be equal to zero, then:
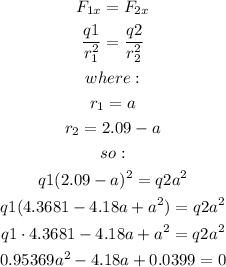
Solve for a:
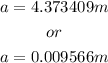
Since the third charge is between the first two charges, the distance must be less than 2.09m
Therefore, the correct option is:
a = 0.009566
Answer:
0.009566 m