Question

Two charges are separated by 2.09 m as follows: -9.14 mC is located at x=0, -46.31 mC is located at 2.09. Where would you place a third charge of -3.78 mC so that the net force on the third change is zero?

Answer 1

Using Coulomb's law

Let:

F1x = Force of the charge of -9.14mC on the charge of -3.78mC

F2x = Force of the charge of -46.31mC on the charge of -3.78mC

So:

`\begin{gathered} F_(1x)=K\cdot(q1\cdot q2)/(r_1^2) \\ F_(2x)=K\cdot(q2\cdot q3)/(r_2^2) \\ where: \\ q1=-9.14*10^(-3)C \\ q2=-3.78*10^(-3)C \\ q3=-46.31*10^(-3)C \end{gathered}`

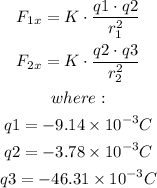
Since the net force on the 3rd charge must be equal to zero, then:

`\begin{gathered} F_(1x)=F_(2x) \\ (q1)/(r_1^2)=(q2)/(r_2^2) \\ where: \\ r_1=a \\ r_2=2.09-a \\ so: \\ q1(2.09-a)^2=q2a^2 \\ q1(4.3681-4.18a+a^2)=q2a^2 \\ q1\cdot4.3681-4.18a+a^2=q2a^2 \\ 0.95369a^2-4.18a+0.0399=0 \end{gathered}`

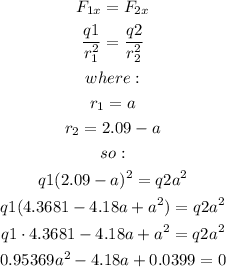
Solve for a:

`\begin{gathered} a=4.373409m \\ or \\ a=0.009566m \end{gathered}`

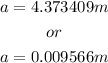
Since the third charge is between the first two charges, the distance must be less than 2.09m

Therefore, the correct option is:

a = 0.009566

Answer:

0.009566 m