Question

X^1/2 x X^2/3Simplify

Answer 1

`\mathbf{x}^{\mathbf{(7)/(6)}}`

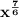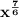
1) Let's simplify the following product:

`x^{(1)/(2)}\cdot x^{(2)/(3)}`

Note that, we can simplify this using the exponent's properties.

2) So we can keep the base and add the exponents:

`x^{(1)/(2)}\cdot x^{(2)/(3)}=x^{(3+4)/(6)}=x^{(7)/(6)}`

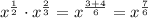
Note that since the denominators were different, we had to resort to the LCM of 2 and 3 and simplify it to one fraction.

3) Hence, the answer is:

`\mathbf{x}^{\mathbf{(7)/(6)}}`