Answer: 1
=====================================================
Work Shown:
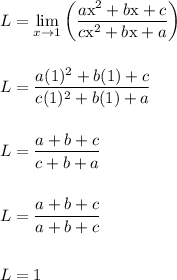
Therefore,
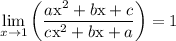
-------------------
Step-by-step explanation:
Apply substitution. Replace each copy of x with 1. We don't have to worry about division by zero errors in this case. After replacing x, we have a+b+c in the numerator and denominator, in which cancel to get us 1 as the final answer.