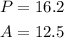To find the perimeter of the trangle, use the formula for te distance between two points to calculate the length of each side of the triangle. Then, add the length of the three sides to calculate the perimeter.
The formula for the distance between two points (x₁,y₁) and (x₂,y₂) is:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
Then, the distance between (0,4) and (2,-1) is:
![\begin{gathered} \sqrt[]{(0-2)^2+(4--1)^2}=\sqrt[]{(-2)^2+(5)^2} \\ =\sqrt[]{4+25} \\ =\sqrt[]{29} \\ \approx5.385 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2c42nae8smttr4vw52cbkm97tf7zkuz5bg.png)
The distance between (2,-1) and (-3,-1) can be found by counting the squares in the picture, since it is a horizontal line. The distance between those points is 5.
The distance from (-3,-1) to (0,4) is:
![\begin{gathered} \sqrt[]{(-3-0)^2+(-1-4)^2} \\ =\sqrt[]{(-3)^2+(-5)^2} \\ =\sqrt[]{9+25} \\ =\sqrt[]{34} \\ \approx5.831 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wbut93cx01vf03be1b8awez6yvib0h5g9k.png)
Add the lengths of the three sides to find the perimeter of the triangle:
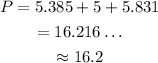
The area of a triangle can be found using the formula:
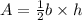
Where b is the base of the triangle and h is the height of the triangle.
Using the horizontal side as the base of the triangle, its height is the perpendicular distance from the vertex (0,4) to the base. By counting squares, we can see that the height of the triangle is 5.
Since the length of the base is also 5, replace b=5 and h=5 to find the area of the triangle:
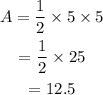
Therefore, the area of the triangle is 12.5 and the perimeter of the triangle is 16.2. The answers are: