AplWe are given that the value of land increases according to the following function:
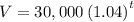
We are asked to determine the value of "t" for which the value of the function is 90000.
to so that we will set the function equal to 90000:
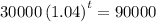
Now, we solve for "t". To do that we will divide both sides by 30000:
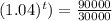
Solving the operations:
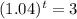
Now, we take the natural logarithm to both sides:
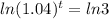
Now, we use the following property of logarithms:
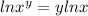
Applying the property we get:
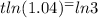
Now, we divide both sides by ln(1.04):
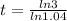
Solving the operations:
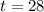
This means that the land will be worth $90000 28 years since 2000, therefore, the year is 2028