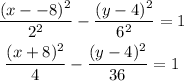Answer
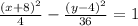
Step-by-step explanation
Since the transverse axis is parallel to the x-axis, this hyperbola opens left/right.
Coordinate of the center, (h, k) = (-8, 4)
The length of the transverse axis = 4 units. This implies that,
a = 4/2 = 2 and b = 12/2 = 6
Please note that the equation of a hyperbola is
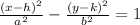
This implies