Question

Information: 44 subjects were treated with garlic. A mean of 3.8 and standard deviation of 18.7. 99% confidence interval.

Answer 1

To calculate the confidence interval, we have the formula:

`CI=\bar{x}\pm z(\frac{s}{\sqrt[]{n}})`

where bar x = mean, z = z-value, s = standard deviation, and n = sample size.

For a 99% confidence interval, the z-value is 2.58. Let's plug in the given information in the question to the formula above.

`CI=3.8\pm2.58(\frac{18.7}{\sqrt[]{44}})`

Then, solve. Let's start by getting the quotient of 18.7 and square root of 44.

`CI=3.8\pm2.58(2.8191)`

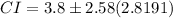
Next, multiply 2.58 and 2.8191.

`CI=3.8\pm7.2733`

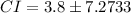
Lastly, separate the plus and minus sign and do the operation.

`\begin{gathered} CI=3.8+7.2733=11.0733\approx11.07 \\ CI=3.8-7.2733=-3.4733\approx-3.47 \end{gathered}`

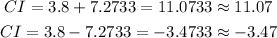
Hence, at 99% confidence interval, the population mean falls between -3.47 mg/dL and 11.07 mg/dL.

`-3.47<\mu<11.07`

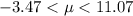
Since our confidence interval includes zero, this means that at some point if experiment is to be rerun again, there's a chance that the garlic treatment did not affect the LDL cholesterol levels. (Option C)