Answer:
(a)V=36πh
Step-by-step explanation:
• Radius = 6 meters
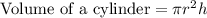
Part A
An equation that represents the volume V as a function of the height h is:

Part B
Using 3.14 as an approximation for π
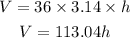
The graph of the function is attached below: (V is on the y-axis and h is on the x-axis).
Part C
The initial equation for volume is:
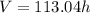
When h=1
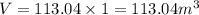
If you double the height of a cylinder, h=2:
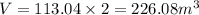
We observe that when the height is doubled, the volume of the cylinder is also doubled.
Part D
The initial equation for volume is:
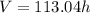
If the height of the cylinder is multiplied by 1/3, we have:
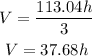
The volume of the cylinder will be divided by 3.
Using the graph, we observe a horizontal stretch of the graph by 1/3.