Question

Select the correct answer. One solution to a quadratic function, g is given. Which statement is true

Answer 1

Given the solution to a quadratic function:

`9-\sqrt[]{2i}`

Let's select the statement that is true.

The given solution (9 - √2i) is a complex conjugate.

For any quadratic function, the complex roots can be expressed as:

`a\pm bi`

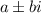
The solution to the quadratic function is:

`9\pm\sqrt[]{2i}`

Therefore the other solution to the quadratic function, g, will be:

`9+\sqrt[]{2i}`

ANSWER:

D. The other solution to function g is 9 + √2i