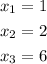Given the function:

You can find the x-intercepts by following these steps:
1. Make the function equal to zero:
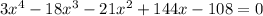
2. Factor the equation:
- Notice that all the terms have 3 in common. Therefore, you can factor it out:
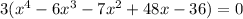
- Rewrite these terms as the Difference between two terms:
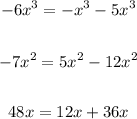
Then:
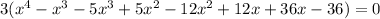
- Make groups of two terms using parentheses:
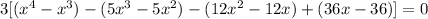
- Factor the Greatest Common Factor of each group out (the greatest factor the terms have in common):
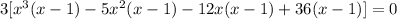
- Factor this common factor out:
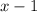
Then:
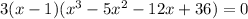
- Rewrite these terms as follows:
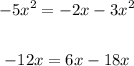
Then:
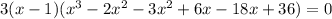
- Make groups of terms:
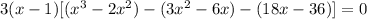
- Factor the Greatest Common Factor of each group out:
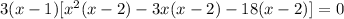
- Factor this factor out:
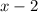
Then:
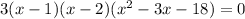
- Factor the Quadratic Expression by following two terms whose Sum is -3 and whose Product is -18. These are 3 and -6. Then:
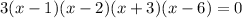
3. Divide both sides of the equation by 3:
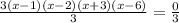
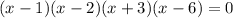
4. Solving for "x", you get the following values:
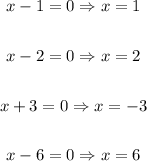
Hence, knowing that you have to reject the negative values, the answer is: