Question

A toy cannon ball is launched from a cannon on top of a platform. The equation h(t) = -3t² + 12t + 15gives the height h, in meters, of the ball t seconds after it is launched. (a)Does the ball reach a height of 16 m?(b)How long does it take the ball to hit the ground?

Answer 1

(a)Yes

(b)5 seconds

Step-by-step explanation:

Given the equation: h(t) = -3t² + 12t + 15

(a)To determine if the ball reaches a height of 16m, we find the maximum height of the cannon ball.

The maximum height occurs at the axis of symmetry.

First, we find the equation of symmetry.

`\begin{gathered} t=-(b)/(2a) \\ =-(12)/(2*-3) \\ =-(12)/(-6) \\ t=2 \end{gathered}`

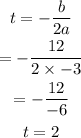
We find h(2).

`\begin{gathered} h(2)=-3(2)^2+12(2)+15 \\ =-12+24+15 \\ =27\text{ meters} \end{gathered}`

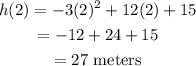
The ball reaches a height of 16 meters since its maximum height is 27 meters.

(b)The ball reaches the ground at the point when h(t)=0.

`\begin{gathered} -3t^2+12t+15=0 \\ -3t^2+15t-3t+15=0 \\ -3t(t-5)-3(t-5)=0 \\ (t-5)(-3t-3)=0 \\ t-5=0\text{ or }-3t-3=0 \\ t=5\text{ or }-3t=3 \\ t=5\text{ or }t=-1 \end{gathered}`

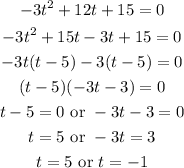
Since time cannot be negative, the ball hits the ground after 5 seconds.