Answer:
(a)Yes
(b)5 seconds
Step-by-step explanation:
Given the equation: h(t) = -3t² + 12t + 15
(a)To determine if the ball reaches a height of 16m, we find the maximum height of the cannon ball.
The maximum height occurs at the axis of symmetry.
First, we find the equation of symmetry.
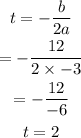
We find h(2).
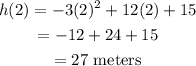
The ball reaches a height of 16 meters since its maximum height is 27 meters.
(b)The ball reaches the ground at the point when h(t)=0.
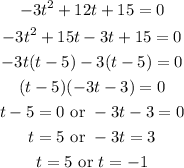
Since time cannot be negative, the ball hits the ground after 5 seconds.