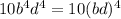Question

Simplify the following expresion by using the law of exponents

Answer 1

We are given the following expression

`(4bd^2)((5)/(2)b^3d^2)`

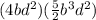
The absense of an operation sign between the parenthesis means that we are multiplying this expression. Note that the expression 4bd² means that we are multiplying 4 by b by d². This means that we are multiplying a lot of terms.

To simplify this expression, first recall the following property of exponents.

`a^b\cdot a^c=a^(b+c)`

That is, when multiplying exponents with the same base, we can simply leave the base and add the exponents.

Since we are multipliying numbers, we con rearrange the expression as follows:

`(4bd^2)((5)/(2)b^3d^2)=(4\cdot(5)/(2))\cdot(b\cdot b^3)\cdot(d^2_{}\cdot d^2)`

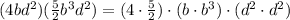
Using the previous property on the middle and right-most term, we get

`(4\cdot(5)/(2))\cdot(b\cdot b^3)\cdot(d^2\cdot d^2)=(4\cdot(5)/(2))\cdot(b^(1+3))\cdot(d^(2+2))=(4\cdot(5)/(2))\cdot b^4_{}\cdot d^4`

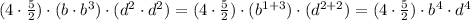
Note that,

`4\cdot(5)/(2)=(4\cdot5)/(2)=(2\cdot2\cdot5)/(2)=2\cdot5=10`

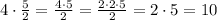
So,

`(4\cdot(5)/(2))b^4d^4=10b^4d^4`

We can simplify this expression even further by using the following property, given numbers a,b,c then

`a^c\cdot b^c=(a\cdot b)^c`

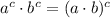
Then, using this, we get

`10b^4d^4=10(bd)^4^{}`