Question

Find the maximum point of the function y = –(x + 4)2 + 2.

Answer 1

Given:

`y=-\left(x+4\right)^2+2`

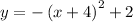
To determine the maximum point of the function,

step 1: Take the first derivative of the function.

`y^(\prime)=-2x-8`

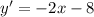
Step 2: Find the critical point of the function.

At the critical point, y' equals zero.

Thus,

`\begin{gathered} -2x-8=0 \\ add\text{ 8 to both sides,} \\ -2x-8+8=0+8 \\ \Rightarrow-2x=8 \\ divide\text{ both sides by -2} \\ (-2x)/(-2)=(8)/(-2) \\ \Rightarrow x=-4 \end{gathered}`

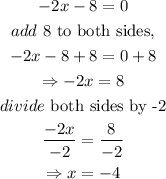
Step 3: Take the second derivative of the function.

Thus, we have

`y^(\prime)^(\prime)=-2`

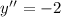
Since y'' is less than zero, it implies that there's a maximum value/point.

step 4:: Evaluate the maximum value of y.

This gives:

`\begin{gathered} y=-(x+2)^2+2 \\ where\text{ x=-4} \\ y=-(-4+4)^2+2=2 \\ \Rightarrow y=2 \end{gathered}`

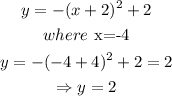
Hence, the maximum point of the function is

`(-4,2)`

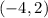
The correct option is