Hello there. To solve this question, we have to remember some properties about probabilities.
Given that buying a pair of shoes and buying a book are independent events and the probability a shopper buys shoes is 0.12 and the probability that a shopper buys a book is 0.10, we want to determine:
The probability that a shopper buys shoes and a book.
For this, say that the events
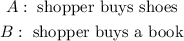
They are independent, which means that
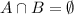
But we're looking for the probability of the shopper buying shoes and a book, therefore the probability of the intersection of events is not zero.
We use the conditional probability to prove that
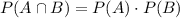
Hence we have that
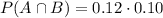
Multiplying the numbers gives you
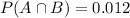
This is the answer to this question and it is contained in the last option.