We multiply the numerator and denominator by the conjugate of the denominator to rationalize it. The conjugate of the denominator is the same expression but with the opposite sign.
![\begin{gathered} \text{ Denominator }=3+\sqrt[]{6} \\ \text{ Conjugate of the denominator }=3-\sqrt[]{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/b28kn7gwide1jacrwmuauxf2uu8m73huo7.png)
Then, we have:
![\begin{gathered} \frac{5}{3+\sqrt[]{6}}=\frac{5}{3+\sqrt[]{6}}\cdot\frac{3-\sqrt[]{6}}{3-\sqrt[]{6}} \\ \frac{5}{3+\sqrt[]{6}}=\frac{5(3-\sqrt[]{6})}{(3+\sqrt[]{6})(3-\sqrt[]{6})} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8sdru2xfxx7ksf8jslpj40ps44j7m48z5c.png)
Now, we apply the difference of squares formula.
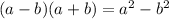
![\begin{gathered} \frac{5}{3+\sqrt[]{6}}=\frac{5\cdot3-5\cdot\sqrt[]{6}}{3^2-(\sqrt[]{6})^2} \\ \frac{5}{3+\sqrt[]{6}}=\frac{15-5\sqrt[]{6}}{9-6} \\ \frac{5}{3+\sqrt[]{6}}=\frac{15-5\sqrt[]{6}}{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5jggqlzrh99j7vfk2ox53shpkuzmbe2ss7.png)
Therefore, after rationalizing the denominator of the given fraction, the new denominator is 3.