We know,
1 penny=1cent.
1 nickel=5 cent.
1 dime=10 cent
1 quarter=25 cent.
1 dollar=100 cent
Given,
There are 143 more dimes than quarters, 3 times as many nickels as quarters
and 8 more than 25 times as many pennies as quarters
Let Q be the number of quarters. So, the number of dimes is,
D=143+Q.
The number of nickels is,
N=3Q.
The number of pennies is,
P=8+25Q.
Let p, n, d, q, t represent respectively the value of penny, nickel, dime, quarter in cents.
Given, the total amount is T=$35.38.
The total amount in cents can be found as,

Hence, the total amount in cents can be expressed as,
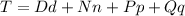
Now put the values in the expression.
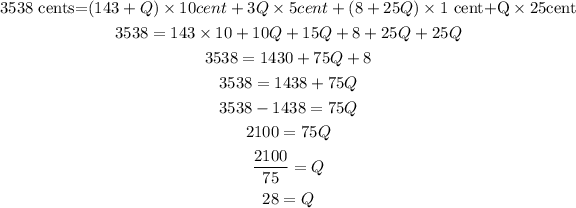
Now, the number of dimes can be calculated as,
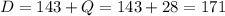
The number of nickels can be calculated as,
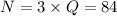
The number of pennies can be calculated as,
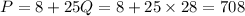
Therefore, there are 28 quarters, 171 dimes, 84 nickels and 708 p