Question

A family has a coin jar that is now full. The children count the change and calculate the total value to be$35.38. Let Q represent the number of quarters and use the information below to find the number of eachcoin.There are:143 more dimes than quarters3 times as many nickels as quarters8 more than 25 times as many pennies as quartersIn the jar there was:Quarters,dimes,nickels, andpennies.

Answer 1

We know,

1 penny=1cent.

1 nickel=5 cent.

1 dime=10 cent

1 quarter=25 cent.

1 dollar=100 cent

Given,

There are 143 more dimes than quarters, 3 times as many nickels as quarters

and 8 more than 25 times as many pennies as quarters

Let Q be the number of quarters. So, the number of dimes is,

D=143+Q.

The number of nickels is,

N=3Q.

The number of pennies is,

P=8+25Q.

Let p, n, d, q, t represent respectively the value of penny, nickel, dime, quarter in cents.

Given, the total amount is T=$35.38.

The total amount in cents can be found as,

`\begin{gathered} T=35.38*100\text{ cents} \\ =3538\text{ cents} \end{gathered}`

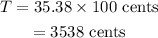
Hence, the total amount in cents can be expressed as,

`T=Dd+Nn+Pp+Qq`

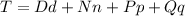
Now put the values in the expression.

`\begin{gathered} 3538\text{ cents=}(143+Q)*10cent+3Q*5cent+(8+25Q)*1\text{ cent+Q}*25\text{cent} \\ 3538=143*10+10Q+15Q+8+25Q_{}+25Q \\ 3538=1430+75Q+8 \\ 3538=1438+75Q \\ 3538-1438=75Q \\ 2100=75Q \\ (2100)/(75)=Q \\ 28=Q \end{gathered}`

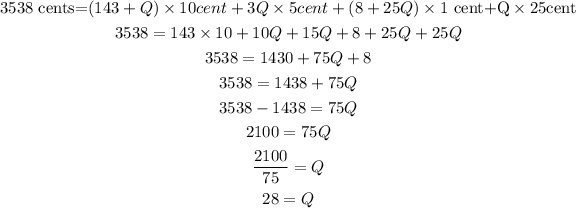
Now, the number of dimes can be calculated as,

`D=143+Q=143+28=171`

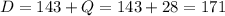
The number of nickels can be calculated as,

`N=3* Q=84`

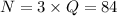
The number of pennies can be calculated as,

`P=8+25Q=8+25*28=708`

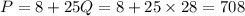
Therefore, there are 28 quarters, 171 dimes, 84 nickels and 708 p