The given information is:
-The dimensions of a box are x, 2x, and 3x.
-Each dimension is increased by 5, then the new dimensions are:
(x+5)
(2x+5)
(3x+5)
The volume of the box is given by the multiplication of its 3 dimensions, then it is:
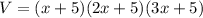
Let's apply the distributive property to this equation:
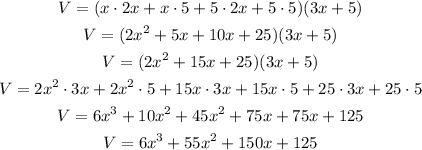
This function above is the volume of the box.