Question

The dimensions of a box are x, 2x, and 3x. Each dimension is increased by 5. Calculate the volume of the box. 623 1 55c2 + 150x + 125 KOD 60 O 6x3 + 125 0 400x3 2x2 + 451 + 125

Answer 1

The given information is:

-The dimensions of a box are x, 2x, and 3x.

-Each dimension is increased by 5, then the new dimensions are:

(x+5)

(2x+5)

(3x+5)

The volume of the box is given by the multiplication of its 3 dimensions, then it is:

`V=(x+5)(2x+5)(3x+5)_{}`

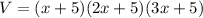
Let's apply the distributive property to this equation:

`\begin{gathered} V=(x\cdot2x+x\cdot5+5\cdot2x+5\cdot5)(3x+5) \\ V=(2x^2+5x+10x+25)(3x+5) \\ V=(2x^2+15x+25)(3x+5) \\ V=2x^2\cdot3x+2x^2\cdot5+15x\cdot3x+15x\cdot5+25\cdot3x+25\cdot5 \\ V=6x^3+10x^2+45x^2+75x+75x+125 \\ V=6x^3+55x^2+150x+125 \end{gathered}`

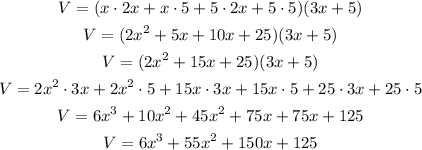
This function above is the volume of the box.