Question

A private jet can fly 2660 miles in four hours with a tailwind, but only 2492 milesin four hours with a headwind.What is the speed of the jet in still air?What is the speed of the wind?Pls see the picture

Answer 1

The Solution:

Let the speed of the jet without the wind be x and the speed of the wind be y.

By formula,

`\text{ Speed (S) =}\frac{\text{ distance (d) }}{\text{ time (t) }}`

So,

With the Tailwind:

d=distance = 2660 miles

t=time = 4 hours

s = speed = (x+y) m/h

Substituting these values in the formula above, we get

`\begin{gathered} (x+y)=(2660)/(4) \\ \\ x+y=665\ldots\text{eqn}(1) \end{gathered}`

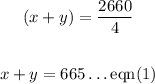
Wind the Headwind:

d = 2492 miles

t = 4 hours

speed = (x-y) m/h

Substituting, we get

`\begin{gathered} (x-y)=(2492)/(4) \\ \\ x-y=623\ldots\text{eqn}(2) \end{gathered}`

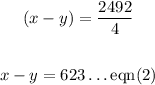
Solving eqn(1) and eqn(2) simultaneously by the Elimination Method.

`\begin{gathered} x+y=665 \\ x-y=623 \\ -------- \\ 2x=1288 \end{gathered}`

Dividing both sides by 2, we get

`x=(1288)/(2)=644\text{ miles/hour}`

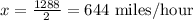
Thus, the speed of the jet is 644 miles/hour.

The speed of the wind ( the value of y):

We shall substitute 644 for x in eqn(1).

`\begin{gathered} 644+y=665 \\ y=665-644 \\ y=21\text{ miles/hour} \end{gathered}`

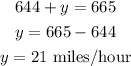
Therefore, the speed of the wind is 21 miles/hour.