The Solution:
Let the speed of the jet without the wind be x and the speed of the wind be y.
By formula,
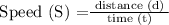
So,
With the Tailwind:
d=distance = 2660 miles
t=time = 4 hours
s = speed = (x+y) m/h
Substituting these values in the formula above, we get
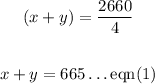
Wind the Headwind:
d = 2492 miles
t = 4 hours
speed = (x-y) m/h
Substituting, we get
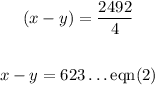
Solving eqn(1) and eqn(2) simultaneously by the Elimination Method.
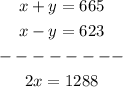
Dividing both sides by 2, we get
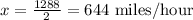
Thus, the speed of the jet is 644 miles/hour.
The speed of the wind ( the value of y):
We shall substitute 644 for x in eqn(1).
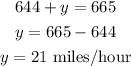
Therefore, the speed of the wind is 21 miles/hour.