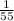Question

The letters in the word PROBABILITY are placed in a box. If two cards are chosen at random, what is theprobability that they will both have the letter B?O 2/121O 1/550 2/11O 1/5

Answer 1

Note that there are 11 letters in the word PROBABILITY, which means 11 possible outcomes or cards. What we have here is going to be a product of two single probabilities.

The probabilty of selecting a letter B in the first experiment shall be;

`\begin{gathered} P\lbrack E\rbrack=\frac{\text{Number of required outcomes}}{Number\text{ of possible outcomes}} \\ \text{Probability of selecting a letter B shall be;} \\ P\lbrack B\rbrack=(2)/(11) \\ \text{Note that there are two letter B} \end{gathered}`

Next we have 10 cards left and for the second experiment we shall have the following;

`\begin{gathered} P\lbrack E\rbrack=\frac{\text{Number of required outcomes}}{Number\text{ of possible outcomes}} \\ P\lbrack B\rbrack=(1)/(10) \\ \text{Note that there is just 1 letter B left after the first experiment} \end{gathered}`

The product of both probabilities shall be;

`\begin{gathered} P\lbrack B\rbrack\cdot P\lbrack B\rbrack=(2)/(11)*(1)/(10) \\ P\lbrack B\rbrack\cdot P\lbrack B\rbrack=(2)/(110) \\ P\lbrack B\rbrack\cdot P\lbrack B\rbrack=(1)/(55) \end{gathered}`

ANSWER:

The probability that they will both have the letter B is the second option;

`(1)/(55)`