Question

CD is formed by C(-5,9) and D(7,5). If line t is the perpendicular bisector of CD, write a linear equation for t in slope-intercept form.

Answer 1

Given that, t is the perpendicular bisector of CD. Therefore, t passes through the midpoint of CD.

The midpoint of c(-5,9) and D(7,5) is,

`\begin{gathered} (x_1+x_2)/(2),(y_1+y_2)/(2) \\ E((-5+7)/(2),(9+5)/(2)) \\ E(1,7) \end{gathered}`

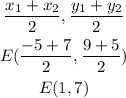
Therefore, the point (1,7) passes through the line t.

The slope of the line segemnet joing (-5,9) and (7,5) is,

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ =(5-9)/(7+5) \\ =-(1)/(3) \end{gathered}`

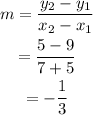
Use the equation m1m2=-1 to calculate the solpe of line t.(Both are perpendicular).

`\begin{gathered} -(1)/(3)m_2=-1 \\ m_2=3 \end{gathered}`

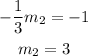
Calculate the equation of line t having slope 3 and point (1,7)

`\begin{gathered} y-y_1=m(x-x_1) \\ y-7=3(x-1) \\ y-7=3x-3 \\ y=3x+4 \end{gathered}`

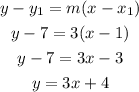
Therefore, the slope intersept form is y=3x+4.