The original area of the triangle is:
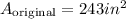
Let's call the original length "l" and the original width "w".
And now we remember the formula to calculate the area of a triangle using the length (or base) and the width (or height):
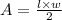
So for the original triangle:
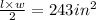
Now, since we are told that the length and width are reduced to 1/3 their orifinal length, the new length is:
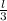
And the new width is:
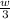
And using this length and width, the area of the new triangle will be calculated as follows:
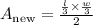
Solving the operations in the numerator:
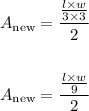
We can re-write this expression as follows:

And we know that for this triangle the expression in parentheses is equal to:
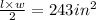
Substituting this into the expression to find the new area:
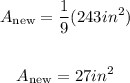
Answer:
the new area is 27 in^2.