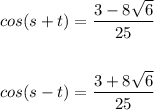Question

This question has been bothering me for a while now, and im studying for a test and not sure what i did wrong

Answer 1

Given:

`cos\text{ }s=(1)/(5);sin\text{ }t=(4)/(5)`

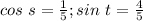
We will find cos (s+t) and cos (s-t)

First, we need to find the sin (s) and cos (t) using the trigonometric Pythagorean identity: sin²x + cos²x = 1

So,

`\begin{gathered} sin\text{ }s=√(1-cos^2s)=(√(24))/(5) \\ \\ cos\text{ }t=√(1-sin^2t)=(3)/(5) \end{gathered}`

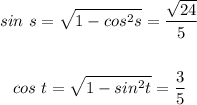
Second, we will find cos(s+t) using the difference identity as follows:

`cos(s+t)=cos\text{ }s*cos\text{ }t-sin\text{ }s*sin\text{ }t`

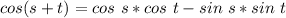
Substitute with the values of the sine and cosine of both angles.

`cos(s+t)=(1)/(5)*(3)/(5)-(√(24))/(5)*(4)/(5)=(3)/(25)-(4√(24))/(25)=(3-8√(6))/(25)`

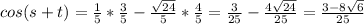
Finally, we will find cos (s - t)

`cos(s-t)=cos\text{ }s*cos\text{ }t+sin\text{ }s*sin\text{ }t`

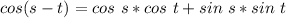
Substitute with the values of the sine and cosine of both angles.

`cos(s-t)=(1)/(5)*(3)/(5)+(√(24))/(5)*(4)/(5)=(3)/(25)+(8√(6))/(25)=(3+8√(6))/(25)`

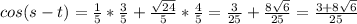
So, the answer will be:

`\begin{gathered} cos(s+t)=(3-8√(6))/(25) \\ \\ cos(s-t)=(3+8√(6))/(25) \end{gathered}`