The given system of equations is
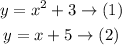
Substitute y in equation (1) by equation (2)
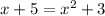
Switch the 2 sides
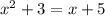
Subtract x from both sides

Subtract 5 from both sides
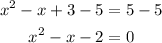
Factor the left side into 2 factors

The factors are (x - 2) and (x + 1)
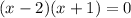
Equate each factor by 0 to find the values of x
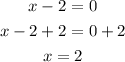
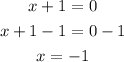
Substitute the values of x in equation (2) to find the values of y
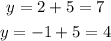
The solutions of the system of equations are
(2, 7) and (-1, 4)