An urn contains balls numbered from 1 through 20
The formula for probability is
![\text{Probability}=\frac{\operatorname{Re}quired\text{ outcome}}{Total\text{ outcome}}]()
Where the total outcome = 20
Since, the first ball was replaced after chosen, then the two events are independent of each other
Let the probability that a first ball is taken be represents by P(F)
Let the probability that a second ball is taken be represents by P(S)
The probability that a first ball is chosen with replacement is
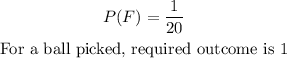
Since there is a replacement, the probability that a second ball is chosen and will be 8 is
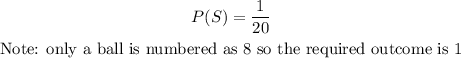
Probability that a first ball is chosen and a second ball is chosen is
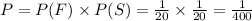
Hence, answer is D