1 Answer

Paul Gorbas · Answer 1 · 2023-05-13T23:17:58+0000

An urn contains balls numbered from 1 through 20

The formula for probability is

$\text{Probability}=\frac{\operatorname{Re}quired\text{ outcome}}{Total\text{ outcome}}$

Where the total outcome = 20

Since, the first ball was replaced after chosen, then the two events are independent of each other

Let the probability that a first ball is taken be represents by P(F)

Let the probability that a second ball is taken be represents by P(S)

The probability that a first ball is chosen with replacement is

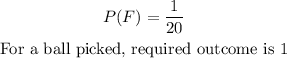
$\begin{gathered} P(F)=(1)/(20) \\ \text{For a ball picked, required outcome is 1} \end{gathered}$

Since there is a replacement, the probability that a second ball is chosen and will be 8 is

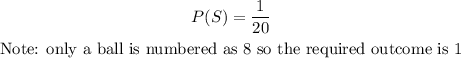
$\begin{gathered} P(S)=(1)/(20) \\ \text{Note: only a ball is numbered as 8 so the required outcome is 1} \\ \end{gathered}$

Probability that a first ball is chosen and a second ball is chosen is

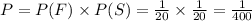
Hence, answer is D

Please log in or register to add a comment.