Given:
a.) Mr. Ramirez purchased 20 concert tickets for a total of $225.
b.) The concert tickets cost $15 for adults and $10 for children under the age of 12.
Let's generate equations on the given scenario where:
a = the number of tickets bought for adults
c = the number of tickets bought for children
We get,
a.) Mr. Ramirez purchased 20 concert tickets for a total of $225.
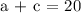
b.) The concert tickets cost $15 for adults and $10 for children under the age of 12.
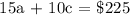
Let's now solve using the Substitution Method:
a + c = 20
a = 20 - c (Substitute to Equation b)
15a + 10c = 225
15(20 - c) + 10c = 225
300 - 15c + 10c = 225
-5c = 225 - 300
-5c = -75
-5c/-5 = -75/-5
c = 15
Therefore, Mr. Ramirez purchased 15 tickets for the children.
For the number of tickets for children:
a + 15 = 20
a = 20 - 15
a = 5
Therefore, Mr. Ramirez purchased 5 tickets for the adults.
In Summary:
Mr. Ramirez bought 15 tickets for children and 5 tickets for adults.