Question

Mr. Ramirez purchased 20 concert tickets for a total of $225. The concert tickets cost $15 for adults and $10 for children under the age of 12. Write and solve a system of equations to represent the given scenario. Use the variables "a" for adults and "c" for children. To earn full credit, show your work using a method explained in the Orientation.

Answer 1

Given:

a.) Mr. Ramirez purchased 20 concert tickets for a total of $225.

b.) The concert tickets cost $15 for adults and $10 for children under the age of 12.

Let's generate equations on the given scenario where:

a = the number of tickets bought for adults

c = the number of tickets bought for children

We get,

a.) Mr. Ramirez purchased 20 concert tickets for a total of $225.

`\text{ a + c = 20}`

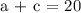
b.) The concert tickets cost $15 for adults and $10 for children under the age of 12.

`\text{ 15a + 10c = \$225}`

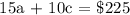
Let's now solve using the Substitution Method:

a + c = 20

a = 20 - c (Substitute to Equation b)

15a + 10c = 225

15(20 - c) + 10c = 225

300 - 15c + 10c = 225

-5c = 225 - 300

-5c = -75

-5c/-5 = -75/-5

c = 15

Therefore, Mr. Ramirez purchased 15 tickets for the children.

For the number of tickets for children:

a + 15 = 20

a = 20 - 15

a = 5

Therefore, Mr. Ramirez purchased 5 tickets for the adults.

In Summary:

Mr. Ramirez bought 15 tickets for children and 5 tickets for adults.