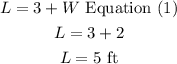Question

Arthur wants to build an enclosure for his rabbits. The enclosure needs to have an area of at least 10 square feet. The length of the enclosure needs to be 3 feet longer than the width. What are the possible lengths of the enclosure?

Answer 1

Length= 5 dft¿¿¿

width =2 ft

Step-by-step explanation

Step 1

Let

L represents the length

W represents the width

then

`\text{Area}=L\cdot W`

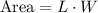
if the enclosure needs to have an area of at least 10 square feet, then

`\begin{gathered} \text{Area}\ge10ft^2 \\ L\cdot W\ge10\text{ Inequality (1)} \end{gathered}`

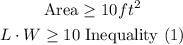
Step 2

The length of the enclosure needs to be 3 feet longer than the width, in other words you have to add 3ft to the width to obtain the length

`L=3+W\text{ Equation (1)}`

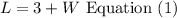
Step 3

replace equation(1) into inequality (1)

`\begin{gathered} L\cdot W\ge10\text{ Inequality (1)} \\ (3+W)\cdot W\ge10 \\ 3W+W^2\ge10 \\ W^2+3W-10\ge0 \end{gathered}`

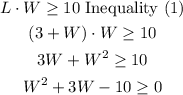
now, we need to factorize, we need two numbers a and b, such

`\begin{gathered} a+b=3 \\ a\cdot b=-10 \\ \text{then} \\ a=5 \\ b=-2 \end{gathered}`

So,

`\begin{gathered} W^2+3W-10\ge0 \\ (W+5)(W-2)\ge0 \\ \end{gathered}`

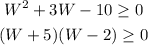
the solutions are

`\begin{gathered} W+5\ge0\text{ and W-2}\ge0 \\ W\ge-5\text{ and W}\ge2 \end{gathered}`

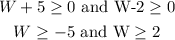
we need a positive value for the width, so we take

`W\ge2`

Now, replace the value of W in equation (1) to find L

`\begin{gathered} L=3+W\text{ Equation (1)} \\ L=3+2 \\ L=5\text{ ft} \end{gathered}`