We have the following expression:
![3\sqrt[]{45}](https://img.qammunity.org/2023/formulas/mathematics/college/l85u5fo4cjwybjmo96344hd30snauw54ks.png)
First, we must find the prime factorization of the number inside the radical:
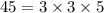
Next, determine the index of the radical. In our case the index is two because it is a square root, which means we need two of a kind:
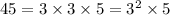
Then, we can move 3 outside the radical, that is
![3\sqrt[]{45}=3\sqrt[]{3^2*5}=3*3\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/zro2iw2d8tdvtbn4wuc1zx2a8iclr9b0iy.png)
and finally, simplify the expression both inside and outside the radical:
![3\sqrt[]{45}=9\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/7b5yu1ws40bq5pi6f0ca5j6bb6zrcvrfks.png)
Then, the answer is