Answer
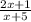
Step-by-step explanation
To simplify this expression, we will factorize each of these equations
6x² - 7x - 5
= 6x² - 10x + 3x - 5
= 2x (3x - 5) + 1 (3x - 5)
= (2x + 1) (3x - 5)
3x² + 10x - 25
= 3x² + 15x - 5x - 25
= 3x (x + 5) - 5 (x + 5)
= (3x - 5) (x + 5)
So, we can write the expression and simplify below
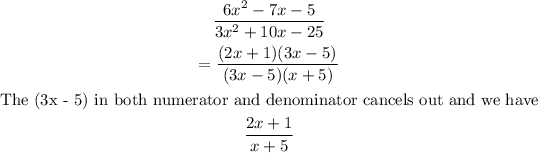
Hope this Helps!!!