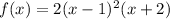Since x=1 is a root of multiplicity 2 and x= -2 is a root with multiplicity 1, our polynomial has the form

where A is an unknown constant.
We can find A by substituting into our last result the given point (0,4), that is,
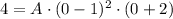
which gives

then, by dividing both sides by 2, we get
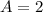
Therefore, the answer is: