Question

The question asks: which descriptions of the figure MUST be true? Select all that apply.

Answer 1

We can check each option.

a) We have to prove that x = 8.

The sides KN and MN should have the same length, so we can write:

`\begin{gathered} KN=MN \\ 7x-4=5x+12 \\ 7x-5x=12+4 \\ 2x=16 \\ x=(16)/(2) \\ x=8 \end{gathered}`

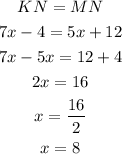
As x has to be 8, this option is true.

b) This option states that KN = 24.

We can test this using the value of x we have just calculated:

`\begin{gathered} KN=7x-4 \\ KN=7\cdot8-4 \\ KN=56-4 \\ KN=52 \end{gathered}`

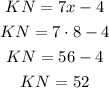
This option is false, as KN = 52.

c) As MN = KN, and KN = 52 (from the last calculation), we can conclude that MN = 52.

Then, this option is true.

d) This option states that KL ≅ ML.

By symmetry, the two sides have to have the same length and are congruent, so this option is true.

e) This option states that LM ≅ LN.

This two segments can not be equal, as they are part of a right angle and the hypotenuse as LN can not have the same length as a leg, like LM.

This option is false.

Answer: the true options are A, C and D.