Given the quadratic equation:
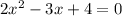
We solve this equation to find the roots. The general solution for a quadratic equation is given by the expression:
![x=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/wyc1fg1v8a6l4tr8e7zi6v658dpql32brp.png)
Looking at the equation, we identify:
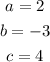
Then, using the general solution formula:
![\begin{gathered} x=\frac{-(-3)\pm\sqrt[]{3^2-4\cdot2\cdot4}}{2\cdot2}=\frac{3\pm\sqrt[]{9-32}}{4} \\ \Rightarrow x_1=\frac{3+\sqrt[]{23}i}{4} \\ \Rightarrow x_2=\frac{3-\sqrt[]{23}i}{4} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gpj45x2exyzhzcn6qcsfrqduq284rr9fe3.png)
Now, we need to know the sum of the squares of x₁ and x₂. Then:
![\begin{gathered} x^2_1+x^2_2=(1)/(16)(9+2\cdot\sqrt[]{23}\cdot i-23+9-2\cdot\sqrt[]{23}\cdot i-23) \\ \Rightarrow=(1)/(16)(18-46)=-(28)/(16)=-(7)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rhvd41ka6hzlvgxk1kkxazgsn1qcu6cb0t.png)