Hello there. To solve this question, we'll have to remember some properties about derivatives.
Given the following function:

We want to take its derivative.
For this, we'll have to apply some rules:
The derivative of a quotient of two continuously differentiable functions is given by the quotient rule:
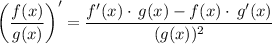
The derivative of the tangent function can be found using the above rule and by knowing the derivatives of sine and cosine. In this case, we obtain the following:
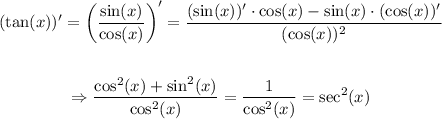
The derivative of a power can be found using the limit definition of a derivative, in this case we obtain:
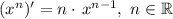
With these rules, we can already solve the question.
First, the derivative is a linear operator, which means that
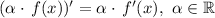
Hence we get that
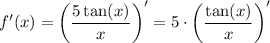
Now, apply the quotient rule
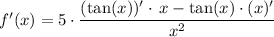
Take the derivative of the tangent and apply the power rule
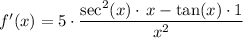
Therefore we get that

Is the answer to this question.